Példafüggvény: $f(x)=(x+3)(x-1)^2$

Az értelmezési tartomány ($D_{f}=R)$ és az értékkészlet $(R_{f}=R)$  meghatározása után megkeressük a fv. zérushelyeit:

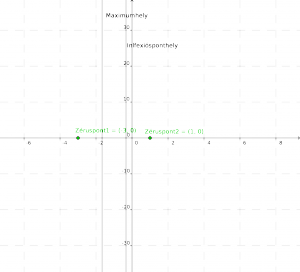
a) $x+3=0$ -> $(-3,0)$

b) $(x-1)^2=0$ -> $(1,0)$

Ábrázolva (zöld pontok):

Kattints a képekre a nagyobb mérethez!

Ezek után megkeressük a fv. első deriváltját a lehetséges szélső értékek meghatározásához:

$f(x)=(x+3)(x-1)^2=(x+3)(x^2-2x+1)=$
$=x^3-2x^2+x+3x^2-6x-3=x^3+x^2-5x+3$

$f'(x)=3x^2+2x-5$

Megkeressük az első derivált zérushelyeit is:

$3x^2+2x-5=0$, amely egy egyszerű másodfokú fv. -> megoldóképlet!

$x_{1,2}=\frac{-2\pm \sqrt{2^2 – 4 \cdot 3 \cdot (-5)}}{2\cdot3}$, amely alapján $x_{1}=-1,\dot{6}$ és $x_{2}=1$

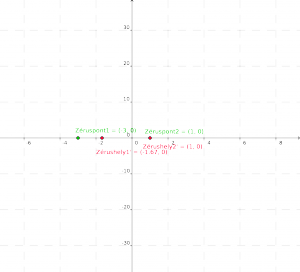Ezek a (pirossal jelölt) zérushelyek az eredeti (f) fv. lehetséges szélső értékei vagy inflexiós pontjai.

Inflexiós pontot ott találunk, ahol a derivált fv. “irányt vált”, tehát annak meredekségének előjele megváltozik. Ez a differenciálszámítás alapján azt jelenti, hogy a deriváltfv. metszi az x tengelyt az adott x értéknél és előjelet vált (negatívból pozitívba fordul, ill. vica versa). Ehhez tekintsük meg a most már ábrázolható f'(x) fv-t:

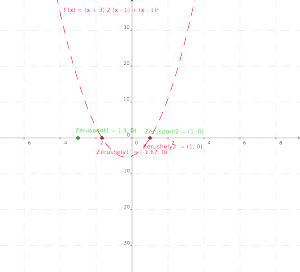Látható, hogy az f'(x) zéruspontjai nem csak érintik az x tengelyt, hanem azon át is haladnak, így az eredeti f(x) fv. lokális szélső értékeit kaptuk meg.

Az előjelváltásból lehet következtetni a szélső érték típusára is: a (-3,0) pontban az első derivált pozitívból negatívba fordul, így egy lokális maximumát találtuk meg az eredeti f(x) fv-nek, míg az (1,0) pontban pont fordítva: lokális minimumot találtunk.

A szélső érték típusát meghatározhatjuk a számított második derivált segítségével (l. alább).

Két ellentétes lokális érték nem fordulhat elő egymás mellett közte inflexiós pont nélkül, ehhez elemezzük a második deriváltat:

$f”(x)=6x+2$

A második derivált, amely egy egyszerű, lineáris fv., zérushellyel rendelkezik a $(-0,\dot{6})$ pontban, amely jelzi, hogy a derivált fv. meredeksége (és ezáltal: az eredeti fv-é is!) irányt vált. Ezek alapján itt is egy jellegzetes pontjára akadtunk az eredeti függvényünknek, sejthetően egy inflexiós pontról van szó.

A szélső értékek vizsgálata történhet a második derivált segítségével: az első derivált zérushelyeit helyettesítjük be a második deriváltfv-be. Ahol $f'(x)=0$ és $f”(x)>0$, ott lokális minimuma, ahol $f'(x)=0$ és $f”(x)<0$, ott lokális maximuma van az eredeti fv-nek.

Ennek végleges teszteléséhez keressük meg az f(x) harmadik deriváltját, amely ha nem egyenlő 0-val, úgy kizárólag inflexiós pontról lehet szó.

$f”'(x)=6$

Ezek alapján ismerjük az eredeti fv. két zérushelyét, egy maximum, egy minimum értékét és egy inflexiós pontját:

, amely alapján felrajzolható az eredeti fv:

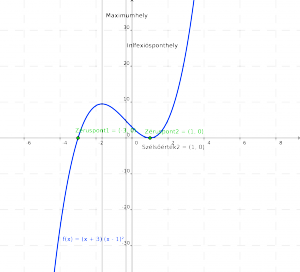És a fentebbiekben ezáltal meghatároztuk az f(x) jellegzetes pontjait.

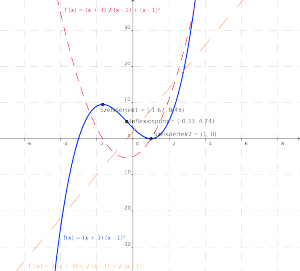
Az f(x), f'(x) és f”(x) függvények ábrázolva az eredeti fv. szélső értékeivel és inflexiós pontjával:

További oldalak, példák:

http://www.geo.u-szeged.hu/~bodis/gis-paper/tani/dem/derivalas/derivalas.html

http://www.kzs.hu/tudastar/Matematika/DERIV_fvmenet_emelt%20szint.ppt