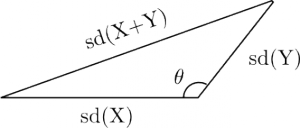Két független változó térbeli megjelenítése nem okozhat problémát, ehhez vegyünk egy egyszerű példát:
Forrás: saját készítésű ábra R-ben (katt a képre a nagyításhoz!)
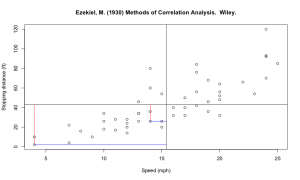
Az ábrán két folytonos változót látunk különböző gépkocsikra vonatkoztatva: a sebesség és a féktávolság (fixme!). Ránézésre egyértelműnek tűnik az a megállapítás, hogy gyorsabb gépjárműhöz nagyobb féktávolság tartozik. Ezt szeretnénk alátámasztani a kovariancia/korreláció meghatározásával.
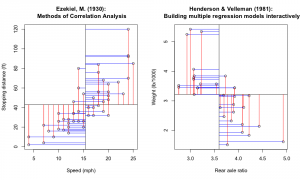
Első körben nézzük meg a változók szórását. A fenti ábrán két kiragadott gépkocsi adatainak a távolságát jelölik a kék és piros szakaszok az átlagos értékektől (fekete vonalak). Amennyiben minden esetben meghatározzuk ezeket a távolságokat, közelebb kerülünk az empirikus szórás meghatározásához:
Forrás: saját készítésű ábra R-ben (katt a képre a nagyításhoz!)
Az átlagtól mért távolságok összegzése során a negatív és pozitív értékek “kioltják egymást”, így a szórás meghatározása során általában az eltérés négyzetével vagy olykor azok abszolútértékével számolunk: $$S^{*}=\sqrt{\frac{\sum_{i=1}^n (x_i-\bar{x})^2}{n-1}}$$
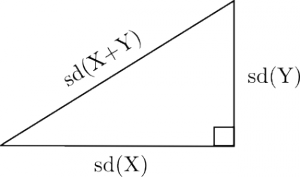
Amennyiben az egyes tengelyeket (változóterekben) az átlagtól való négyzetes eltérések átlagát (magyarán: szórást) ábrázoljuk, úgy független változók esetében az együttes szórást is könnyen meghatározhatjuk:
Forrás: John D. Cock [4]
Lévén, hogy a két változó független, a két szórás által bezárt szög az ábrán 90 fok, így az ismert tétel alapján: $$VAR(X+Y) = VAR(X) + VAR(Y)$$
Amely összefüggés elméleti úton is könnyen bizonyítható: független változók esetében a kovariancia minden esetben 0, így annak nincs módosító hatása a fenteb bemutatott varianciára.
Összefüggést mutató változók estében azonban az ábra módosul és a Pitagorasz-tétel nem alkalmazható:
Forrás: John D. Cock [4]
Így a közös variancia meghatározása is módosul. További részletekkel kapcsolatban lásd az eredeti forrást [4]!