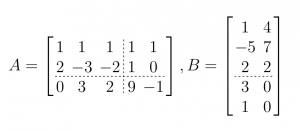$$A=\begin{bmatrix}
1 & 2 & 0\\
2&2&1\\
1&2&0
\end{bmatrix}
\, B=\begin{bmatrix}
1 & 3\\
2&4\\
1&2
\end{bmatrix}
\, C=\begin{bmatrix}
2 & 0\\
0&2
\end{bmatrix}
$$
1. Végezze el a követkető műveleteket:
- $A \cdot B$
- $C \cdot A$
- $B \cdot A$
- $C \cdot B$
- $B \cdot C$
- $3A \cdot B – A$
Letöltés kép formátumban [1] abban az esetben, ha a fenti feladat nem olvasható.
Segédprogram az ellenőrzéshez: jimmysie.com [2]
—
2. Szorozza össze az alábbi particionált mátrixokat!